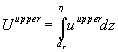Robert H. Weisberg*

Zhenjiang Li

And

Frank Muller-Karger

College of Marine Science

University of South Florida

St. Petersburg, Florida 33701

Final, April 2001

_______________________

* Corresponding author address: Dr. Robert H. Weisberg, College of Marine Science, University of South Florida, 140 Seventh Avenue South, St. Petersburg, Florida 33701. Email: weisberg@marine.usf.edu

Abstract.

We compare in-situ velocity and sea level data with a model simulation for the west Florida continental shelf during April 1998. Responses for three periods of downwelling and upwelling favorable winds are documented. Velocity profiles show coastal jets in the along-shelf direction that are accompanied by oppositely directed upper and lower layer flows in the across-shelf direction. These along- and across-shelf currents and their associated vertical velocity comprise the fully three-dimensional inner-shelf responses to local wind forcing. The responses are sensitive to stratification. Large velocity vector turning occurs under stratified conditions, whereas less turning occurs under well-mixed conditions. With an initial density field representative of April 1998 the model simulates velocity and sea level variations that agree with the observations. Without stratification substantial mismatches occur, both for currents and sea level. Local momentum input is a primary forcing agent for the inner-shelf circulation when the shelf is wide enough to distinguish the inner-shelf from the shelf-break. Inner-shelf responses, however, depend on the density field, which depends on local and offshore buoyancy fluxes. Modeling the inner-shelf responses to wind forcing requires maintenance of the density field through data assimilation and adequate surface, offshore, and land-derived buoyancy inputs.

Dynamical analyses define the inner-shelf as the region where the surface and bottom boundary layers are important in the momentum balance. Kinematically, this is where the surface Ekman layer divergence, fed by the bottom Ekman layer convergence, or conversely, sets up the across-shelf pressure gradient. With respect to vertically integrated vorticity, the inner-shelf is where bottom stress torque tends to balance bottom pressure torque, as contrasted with the shelf-break where the primary balance is between bottom pressure torque and the rate of change of relative vorticity.

Under stratified conditions the inner-shelf responds asymmetrically to upwelling and downwelling favorable winds, with the offshore scale and magnitude of the responses for upwelling favorable winds both being larger than for downwelling favorable winds. This asymmetry is a consequence of the bottom Ekman layer. With respect to the streamwise vorticity component, buoyancy torque by isopycnals bending into the bottom adds constructively (destructively) with planetary vorticity tilting by the sheared coastal jet under upwelling (downwelling) favorable winds causing the asymmetry. Such asymmetry may have important ramifications for material property distributions on the shelf.

Continental shelf circulation results from both local and offshore forcing. Local forcing is by momentum and buoyancy input at the sea surface and buoyancy input at the land boundary. Offshore forcing is by momentum and buoyancy input at the shelf-break. The partition of influence between these contributing factors varies with shelf location and geometry, and nowhere is this partition quantitatively accounted for. How continental shelves are forced thus remains a fundamental question for both the circulation and for the biological, chemical, and geological consequences of the circulation.

The west Florida shelf (WFS) is an end member in the ensemble of continental shelves for which local forcing may be presumed to be of primary importance. This is because the WFS is wide enough for its inner-shelf to be distinguished from the shelf-break. Given the complex nature of continental shelves and the limitations of both in-situ data and models, it is useful to simplify the circulation problem by isolating factors and questioning how well a given data set can be explained by these factors. Along this vein, we ask how well coastal sea level and inner-shelf currents can be explained by the influence of local wind forcing alone. We compare in-situ data from April 1998 with a numerical model driven by observed time varying, but spatially uniform, winds. Our results suggest that inner-shelf currents may be accounted for by local wind forcing, given an appropriately specified initial density field. The density field, however, is shown to play an important role, and since the density field is determined by a combination of offshore and local buoyancy forcing, all such factors must be treated in order to produce useful model products.

The paper is organized as follows. Section 2 reviews background materials on the response of a continental shelf to synoptic wind forcing. Section 3 introduces the in-situ data and the model used to simulate these data. Comparisons between model results and data are given in section 4. Motivated by these comparisons, albeit at limited observational locations, we expand upon the model flow field kinematics in section 5, where fully three-dimensional structures are shown. For brevity, we emphasize one complete cycle of responses to successive downwelling and upwelling favorable winds, and an asymmetry between upwelling and downwelling responses is noted. Section 6 then exploits the model fields to develop the momentum and vorticity balances that help to define the inner-shelf separate from the shelf break. The results are summarized in section 7, where, along with discussing the asymmetry, it is recognized that the synoptic and seasonal scale variability can not be fully separated since responses of one depends upon the density field provided by the other. This is true for sea level, and more so for currents.

Continental shelves are dynamically complex. In relatively deep water the surface and bottom boundary layers are separated by a bottom slope constrained geostrophic flow. As the water depth decreases towards the coast the surface and bottom boundary layers tend to merge across the geostrophic interior. Here, we define the inner-shelf as the near-coastal region where the surface and bottom boundary layers are dynamically important. Our definition is somewhat different from that given by Lentz (1994), and this difference will be clarified in section 6. These boundary layer influences, coupled with the coastline constraint, result in kinematical and dynamical characteristics of the inner-shelf that may differ markedly from those occurring farther offshore. Generally, for synoptic scale variability where wind stress is the principal motive agent, the inner-shelf reacts to the presence of the coast through the establishment of a surface pressure gradient. This occurs through divergence brought about by surface and bottom Ekman layer transports (e.g., Gill, 1982, p394), and recent evidence for such adjustment on the WFS is given by the upwelling case study of Weisberg et al. (2000). Regularly occurring sub-tidal sea level variations show this adjustment to be a common feature of all shelves.

Descriptions of inner-shelf variability have emerged largely from observations on the continental shelves and Great Lakes of North America. Csanady (1982), Walsh (1988), and Brink et al. (1998) provide overviews, and recent representative works from different regions include those of Lentz (1994), Smith (1995), Weisberg et al. (1996), Weatherly and Thistle, (1997), Yankovsky and Garvine (1998), Lentz et al. (1999), and Munchow and Chant (2000). Insights on the dynamics of the inner-shelf are found in the analytical treatment of Mitchum and Clarke (1986). The complex nature of turbulent boundary layers, however, limits the use of analytical techniques, and this has led to numerical model studies of inner-shelf turbulence in simulations of one or two dimensions (e.g., Weatherly and Martin, 1978; Allen et al., 1995; Lentz, 1995). Two dimensions, however, exclude the interactions that may occur between local and large-scale processes and the possibility that the dynamical interactions controlling divergence and vertical motion may vary in the along-shelf direction. For example, in contrast with the two-dimensional circulation pattern of equal and opposite upper and lower layer flows reported by Lentz (1994) for the northern California coast, Munchow and Chant (2000) report a fully three-dimensional flow with a net across-shelf transport for the New Jersey coast. Three-dimensionality there is attributed to an along-shelf pressure gradient force due to coastal geometry and baroclinicity. Long-wave models that assume a boundary condition of no net across-shelf flow at some distance from the coast (e.g., Clarke and Van Gorder, 1986; Lopez and Clarke, 1989) are to some extent contrary to these findings, and additional sensitivity studies such as Samelson (1997) are warranted. While the general physical concepts espoused in all of these studies apply, it is becoming increasingly clear that each individual continental shelf environment is somewhat unique, and that the region of the inner-shelf, where important across-shelf transports occur, requires better understanding.

Exploratory measurements of inner-shelf velocity profiles on the WFS were initiated in November 1996 with the deployment on the 20 m isobath offshore of Sarasota, FL of a bottom-mounted 300 kHz acoustic Doppler current profiler (ADCP) manufactured by RD Instruments, Inc. Using 0.5 m bin spacing, and after editing surface effects, the data set yielded horizontal velocity profiles between depths of 2.5 m to 16 m. Ancillary data sets include sea level from the NOAA tide gauge at St. Petersburg, FL, surface winds from the NOAA buoy number 42036 located at mid-shelf, and velocity profile data from a buoy located at the 50 m isobath. These measurement locations are shown in Figure 1. The data collection effort was initially unsupported by hydrographic data. Through efforts by the Mote Marine Laboratory (G. Kirkpatrick, personal communication, 1998) and the University of South Florida, monthly hydrographic sections were initiated in March 1998.

Co-variations in winds, sea level, and currents occur throughout the record, as expected from previous WFS shelf observations (e.g., Mitchum and Sturges, 1982). A new finding is the variability in the relative turning of the velocity vectors with depth for each synoptic weather event. Responses to upwelling favorable winds generally show onshore flow near the bottom and offshore flow near the surface, and conversely for responses to downwelling favorable winds. These responses are oftentimes accompanied by bottom temperature changes. Once the supportive hydrographic sections commenced it became clear that the velocity vector turning is related to the density stratification. April 1998 is a particularly interesting month with a succession of synoptic weather events and large velocity vector turning. We focus our attention on this month for a comparison between the in-situ data and a numerical model simulation.

The April 1998 data are shown in Figure 2. With emphasis on the time scales of the synoptic weather variations, all of the data are low-pass filtered to remove oscillations at time scales shorter than 36 hours (subsequent model results are also low-pass filtered). Provided are velocity component isotachs for the along-shelf and across-shelf directions, coastal sea level, wind velocity vectors, and wind stress vectors. Along-shelf is defined as 333⁰ relative to the true north. Clear contours are in this up-coast direction and shaded contours are in the reciprocal down-coast direction. For the across-shelf component clear (shaded) contours are directed onshore (offshore). The wind velocity (stress) variations for April 1998 are primarily in the along-shelf direction. Upwelling and downwelling favorable winds are observed over three distinctive periods, and sea level responds to each of these. In the along-shelf direction, each wind change gives rise to a coastal jet of varying vertical structure, i.e., some show subsurface maxima while others show surface maxima. Accompanying the coastal jets are opposing onshore and offshore flows over the upper and lower portions of the water column. The most pronounced response occurs on April 12 when the upwelling favorable winds are largest causing a coastal jet of magnitude 0.6 ms^-1 with onshore (offshore) flow in the bottom (surface) Ekman layer exceeding 0.2 ms^-1. Although the wind stress magnitudes do not differ much from downwelling to upwelling events (April 12 being an exception), the responses in the currents to the upwelling winds are larger in all three cases than the responses to the downwelling winds. A response asymmetry on the WFS is thus observed. Asymmetric behavior in bottom boundary layer thickness has been reported elsewhere (e.g., Trowbridge and Lentz, 1991 and Lentz and Trowbridge, 1991 for the northern California coast), and the destabilizing or stabilizing influences of either down or up slope density transports, respectively, has been offered in explanation. As we will discuss, however, these boundary layer turbulence arguments do not explain the response asymmetry reported here.

We employ the Princeton Ocean Model (Blumberg and Mellor, 1987) based on the following attributes. As a primitive equation model, it allows us to diagnose dynamical balances. Its vertical sigma coordinate helps to resolve the flow structures on a gently sloping shelf, and its horizontal orthogonal curvilinear coordinates allows the model grid to conform to topography. By parameterizing friction with an embedded turbulence closure sub-model (Mellor and Yamada, 1982) the frictional forces evolve with the flow and density fields.

The model domain (Figure 1) extends about 750 km along-shelf from the Florida Panhandle to the Florida Keys and about 400 km offshore from the coast. It covers the entire WFS and part of the eastern Gulf of Mexico so that the shelf-break region is resolved. Realistic shelf bathymetry from the National Center for Atmospheric Research is used with 1500 m being the maximum depth beyond the shelf-break and 5 m being the minimum depth at the coastline. The horizontal grids range in size from 6.5 km to 15 km, with an average of 9 km. 16 sigma levels are used in the vertical, distributed logarithmically about the middle to achieve finer resolution of the surface and bottom boundary layers relative to the interior. Other WFS applications of this model grid, along with discussions of the open boundary conditions, are given by Li (1998) and Li and Weisberg (1999a,b).

The model is forced from mid-March through April 1998 by a spatially uniform, time-dependent wind stress. The wind stress components are computed from the in-situ wind velocity vectors observed at the NOAA buoy using a wind speed dependent drag coefficient (Wu, 1980). Forcings by surface heat and coastal buoyancy fluxes are excluded due to a lack of data.

To initialize the density field we use hydrographic sections from March and May 1998; April 1998 hydrography is not available. Each section shows a well-defined pycnocline. On this basis we initialize the model density field with a 4 sigma-t density change that spans 20 m in the vertical, centered on 20 m depth. To avoid specious baroclinic adjustments, this initial density field is input without horizontal gradient. Subsequent density field evolution occurs in dynamical balance with the applied forcing. A twin experiment with density set constant at 1023 kgm^-3 is also performed to compare the responses under stratified and unstratified conditions. Clarke and Brink (1985), through scale analysis of the shallow water equations, show that the response of a wide shelf [with small Burger number, (L_R/L)², where L_R is the Rossby radius of deformation at the shelf-break and L is the shelf width] to synoptic wind fluctuations should be barotropic. Mitchum and Clarke (1986) suggest that (L_R/L)² <10^-2 for the WFS, and this magnitude is consistent with the stratification used here. The stratified and constant density experiments provide an opportunity to examine this barotropic response concept with a primitive equation model. 15 days of model start up is performed using observed winds prior to sampling the model results for April 1998. Since we find the pressure field response to be largely barotropic, consistent with the Burger number argument, the spin up time is on the order of a pendulum day and much less than the 15 days that we used.

Comparisons between sea level observed and modeled at St. Petersburg, FL for the month of April 1998 are shown in Figure 3. The upper and middle panels are for the constant density and stratified cases, respectively, and the lower panel shows the wind stress vector time series used to force the model. Agreement is very good for the stratified case; it is not as good for the constant density case. While the general patterns of sea level responses to upwelling and downwelling favorable winds are replicated in both cases, considerable quantitative mismatch exists between in the model responses and the observations for the constant density case. In particular, the overestimate for the upwelling response around day 23 implies an excessive across-shelf volume transport over the inner-shelf region during this event. Since a vertically integrated across-shelf volume transport in excess of the volumetric rate of sea level change can only occur in a three-dimensional flow, such disparity on agreements with in-situ data between the stratified and constant density model simulations implies that stratification significantly affects the three-dimensional flow field.

Modeled along-shelf and across-shelf components of velocity from the 20 m isobath off Sarasota, FL are shown in Figure 4a. As is the case for sea level under stratified conditions, the model reproduces the general pattern evolution of the observed velocity component variations (Figure 2). All three upwelling favorable wind events drive down-coast jets with vertical structures similar to those observed, some with subsurface and others with near surface maxima. These down-coast jets are accompanied by onshore (offshore) flow over the lower (upper) portion of the water column. Similar statements apply for the responses to the downwelling favorable wind events, i.e., up-coast jets and across-shelf flow reversals with depth. While the pattern evolutions for the modeled and observed currents are generally similar, differences in details exist for several reasons. First, the model simulations are highly dependent upon stratification, and our initial stratification is merely a guess based upon limited measurements. Second, no provision is made for (unknown) surface heat fluxes or for correcting inevitable departures of the model stratification from nature over the course of the 45-day integration. Third, we use spatially uniform winds when the spatial structure of each synoptic weather system may be different. Despite these shortcomings, the quantitative agreements are surprisingly good, with the best agreements occurring during the downwelling/upwelling sequence of April 7-13. Here the model underestimates the magnitude of the along- and across-shelf components by about 20%. For other sequences this magnitude mismatch is either larger or smaller, and for the reasons stated above there is little gained by more detailed comparisons. One clear deficiency comparing the model with the data lies within the upper 3 m of the water column where there is no data. The model purports large vertical shear over the upper few meters because its turbulence closure routine yields small eddy viscosity (turbulence length scale is zero at the surface). Whether or not such near surface shear is realistic remains to be determined.

Also depicted in Figure 4a are the modeled isopycnal variations. Relative maxima in isopcynal displacements occur when the across-shelf component is zero suggesting that advective changes through horizontal divergence and vertical velocity are the primary contributors. Across-shelf advection over the lower portion of the water column occurs as a boundary layer response to the coastal jet. Since the coastal jet tends to be maximum when the sea level response is maximum, across-shelf and vertical advection are also maxima at that time. Thus, upwelling and downwelling isopycnal displacement maxima occur at the transitions between upwelling and downwelling favorable winds, accounting for the lag between the isopycnal displacements and sea level. This phase relationship constrasts that of an inviscid, standing baroclinic mode for which the isopycnal and sea level responses occur in an anti-phase relationship, demonstrating the importance of the frictional boundary layers. By not imposing a surface heat flux the isopycnals also tend to slope up with time reducing the stratification.

As with sea level, the twin experiment without stratification yields results for the currents (Figure 4b) that are both qualitatively and quantitatively different from the observations. For the along-shelf component the vertical shear is much more uniform with depth, but the more interesting contrast is in the across-shelf component. Without stratification there is very little turning in the surface and bottom boundary layers, and hence there is very little across-shelf circulation relative to the results with stratification. This behavior for the across-shelf component mimics the longer term observational record that shows pronounced velocity vector turning during times of anticipated stratification versus little turning during times when the water column is expected to be well mixed.

Based on the general agreements between the in-situ data and the stratified model results we now use the model to discuss the flow field kinematics and dynamics with emphasis on the downwelling/upwelling response sequence from April 7-14.

The order of presentation includes planar views of sea level, cross-sections of velocity and density at the Sarasota transect, and planar views of currents. We begin with daily snapshots of sea level from day 7 through day 14 (Figure 5a) for the stratified experiment. Peak downwelling and upwelling responses in the sea level fields (as with all other fields) appear on days 9 and 12, respectively. During these peaks the set-down at the coast for the upwelling response in general is more than a factor of two larger than the set up at the coast for the downwelling response. Moreover, the offshore scale for the upwelling response largely exceeds that for the downwelling response. The transitions to these peak responses show along- and across-shelf surface height gradients of comparable magnitude. While no clear sense of propagation emerges, it does appear that the along-shelf variations in geometry, particularly the relatively narrow shelf in the north and the partial closure by the Florida Keys in the south, play roles in determining the sea level adjustments. The end results are monotonic sea level slopes with coastal maxima, but the transitions to these end states are more convoluted, suggestive of complicated flow patterns.

Similar plots for the constant density experiment are given in Figure 5b. Contrasted with the asymmetric responses of Figure5a (in both magnitude and offshore scale), the constant density experiment yields sea level displacement magnitudes that are nearly proportionate with the wind stress and that have comparable offshore scales for either upwelling or downwelling.

Cross-sections for the along-shelf, across-shelf, and vertical velocity components, and density offshore of Sarasota, FL. are shown in Figure 6a. Our focus is again on the day 9 and day 12 peak responses. On day 9 we see an up-coast jet in the along-shelf component, with onshore flow over the upper half and offshore flow over the lower half of the water column in the across-shelf component, and with downwelling occurring synchronously with the offshore flow. In a parallel, but opposite sense, on day 12 we see a down-coast jet in the along-shelf component, with offshore flow over the upper half and onshore flow over the lower half of the water column in the across-shelf component, and with upwelling occurring synchronously with the onshore flow. Due to the frictional effects of the boundary layers the coastal jet has a vertical shear structure with isotachs bending offshore with depth. This accounts for the subsurface maxima that occur in both the in-situ data and the model simulation. In summing the geostrophic interior with the frictional boundary layer flows the velocity vector turns counterclockwise over most of the water column. This is shown for the WFS by Weisberg et al. (2000) and for the New Jersey shelf by Munchow and Chant (2000). As is the case for sea level, the magnitudes and offshore scale for the peak upwelling response are substantially larger than for the peak of the downwelling response. Since the bottom Ekman layer is a response to the coastal jet, across-shelf transports over the lower portion of water occur over the entire offshore extent of the coastal jet for either upwelling or downwelling situations. Since the upwelling response exists over a larger offshore scale than the downwelling response, the across-shelf transports of water for upwelling occur over larger distances than for downwelling.

Similar plots for the constant density experiment are given in Figure 6b. As found for sea level, the asymmetry in the currents under stratified conditions is replaced by a more proportionate response under constant density. With the offshore scales of the coastal jet the surface displacement being equal, the difference in scales for the upwelling and downwelling responses under stratified and constant density conditions parallels that in Figures 5a, b.

Evidence for this model-based assertion of asymmetry exists in simultaneous in-situ data that were collected on the 50 m isobath (Figure 7). The same coastal jets as seen in shallower water (Figure 2) appear here, but with less vertical structure, as in the model. For each wind-driven flow reversal we see that the near surface Ekman layer response (extending down to about 20 m depth) is larger than the near bottom Ekman layer response, also consistent with the model. Moreover, for the peak downwelling response around day 9 we see nearly zero across-shelf flow in the bottom Ekman layer versus about 0.05 msec^-1 onshore flow in the bottom Ekman layer for the peak upwelling response around day 12. These observations are consistent with larger offshore extents for the surface height field and the coastal jet under upwelling favorable winds.

The horizontal structure of the velocity field is complex. Horizontal velocity vector maps for the depth average, near surface, mid-depth, and near bottom fields are shown in the Figure 8 panels a-d, respectively, for the day 9 peak downwelling response. The depth average flow is the simplest of the fields. An up-coast directed jet, confined to the proximity of the shore, is seen with maximum speeds occurring where the sea surface height gradient is maximum. The jet is fed by surface Ekman layer transports that are only partially offset by bottom Ekman layer transports since the bottom Ekman layer is effected only where the surface height gradient and coastal jet are established. Thus the coastal jet accelerates downstream. The character of the near bottom flow also changes from the inner-shelf region, where it is related to the coastal jet, to the shelf break region where it arises by topographic wave variability. The origin of these near bottom flow variations will be evident in the section 6 dynamical analyses. The mid-depth vectors look very similar to the depth average vectors since there the across-shelf flows due to the opposing surface and bottom Ekman layer flows are minimal.

A parallel set of velocity maps are given in Figure 9 for the day 12 peak upwelling response. Similarities exist with Figure 8 (albeit with opposite sign). Contrasting these two figures, however, is the larger offshore scale for the upwelling fields. Strong onshore flows in the bottom Ekman layer exist out to about the 100 m isobath, particularly in the northern part of the domain where the magnitude of the coastal jet is largest. Bottom Ekman layer flows in the southern portion of the domain are reduced by the adverse pressure gradient due to the partial closure by the Florida Keys. Stratification also tends to promote regions of flow field confluence as seen at mid-depth.

A result of the flow field kinematics in switching from downwelling to upwelling favorable winds is manifest in sea surface temperature (SST). Figures 10a, b show satellite AVHRR SST images on April 10 and 13 when the downwelling and upwelling circulations, respectively, culminate in isopycnal displacement maxima. The month of April, in general, shows a cold tongue that extends down-coast at mid-shelf from a region of seasonally coldest SST in the northeastern Gulf of Mexico. Associated with this boreal spring cold tongue is a chlorophyll plume, referred to as the "green river" by Gilbes et al. (1995). This cold tongue is evident on April 10 with warmer waters both inshore and offshore. Transitioning from downwelling to upwelling winds, the cold tongue on April 13 is greatly amplified and the inshore waters are several degrees colder than on April 10. A region of locally coldest SST is also seen south of Tampa Bay on about the 25 m isobath consistent both with the region of maximum vertical velocity in Figure 6a and with the upwelling case study results of Weisberg et al. (2000). Farther south is a diminution of cold SST consistent with the bottom Ekman layer inhibition by adverse pressure gradient shown in Figure 9. Right at the shoreline in the Florida Big Bend region and along the Florida Panhandle west of Apalachicola Bay we also see eruptions of cold water to the surface. While we do not imply that surface heat flux is not a contributing factor, these SST changes are consistent with the kinematical features of the numerical model simulation described in this section.

We begin with vertically integrated momentum and mass balances (Figure 11) calculated at the 20 m isobath offshore from Sarasota, FL. The wind stress is the lead term in the along-shelf direction (panel a). This causes a local acceleration as the currents tend to adjust to the time varying winds, followed by an along-shelf pressure gradient, a bottom stress, and a Coriolis acceleration, with all of these response terms being of comparable magnitude (although the along-shelf pressure gradient is generally the largest of these). In a purely two dimensional flow the bottom stress would be comparable to the surface stress, whereas in this three-dimensional result the bottom stress is no larger than the other secondary terms. The vertically integrated across-shelf momentum balance (panel b) is much simpler (note the scale change between panels a and b). Here the vertically integrated flow is essentially geostrophic since the ageostrophic contributions from the surface and bottom Ekman layers tend to cancel. The magnitudes of the terms in the across-shelf momentum balance are about a factor of four larger than those in the along-shelf momentum balance.

The three-dimensionality of the flow field is also evident in the vertically integrated across-shelf mass transport (panel c). The four time series are: 1) the Ekman transport associated with the wind stress, 2) the vertically integrated upper and 3) lower layer transports directed either onshore or offshore depending on wind stress, and 4) the total vertically integrated transport. The Ekman transport is computed as , where is the along-shelf component of the wind stress. The upper and lower layer transports are defined as 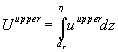, , where u is the velocity component in the across-shelf direction, is the depth at which the across-shelf flow reverses direction, is the free surface elevation, and is the mean water depth. The net across-shelf transport is . The upper layer transport is always less than the Ekman transport because the 20 m isobath is within the inner-shelf where there occurs an upper layer across-shelf transport divergence along with the surface slope set-up. Seaward of the inner-shelf the upper layer transport is comparable to the Ekman transport. The upper layer transport at this particular location is generally over compensated for by the lower layer transport. A contributing factor is the along-shelf pressure gradient that supports an across-shelf geostrophic transport. The along-shelf pressure gradient appears to be larger for upwelling favorable winds than for downwelling favorable winds (panel a). With mass convergence/divergence inferred in the across-shelf direction there must be a mass divergence/convergence in the along-shelf direction to maintain continuity. The coastal jets offshore of Sarasota, FL are therefore spatially accelerating jets, and a consequence of this for upwelling favorable winds is an increase in the intensity of upwelling over what would occur without the spatial acceleration. This is consistent with the region of maximum surface cooling shown in Figure 10b.

An asymmetry in across-shelf transport between upwelling and downwelling is also evident in panel c. This asymmetry arises from the bottom Ekman layer as demonstrated by the ageostrophic portion of the across-shelf momentum balance (panel d). The ageostrophic part is defined as the residual after adding the Coriolis and pressure gradient terms. Both the magnitude and vertical extent of the ageostrophic residual that comprises the bottom Ekman layer at this location are larger for the three upwelling events than for the downwelling events (in particular, compare the April 9 and 12 patterns). This finding is opposite to what is expected from stability arguments for up and down slope flows in a stratified fluid (Trowbridge and Lentz, 1991). Here the bottom boundary layer is consistently larger for upwelling than for downwelling conditions!

To further explore these issues we analyze the across-shelf momentum balance over the Sarasota, FL. transect. Figure 12 shows the results for the peak downwelling event of April 9. Eight panels provide the sequential order of terms that comprise the momentum balance in this coordinate direction. Panels a and b are the Coriolis and pressure gradient terms. Their sum (the ageostrophic residual) is given in panel c for comparison with the frictional terms of panel d (where friction is almost entirely of vertical origin). The sum of panels c and d, in panel e, is for comparison with the advective acceleration terms in panel f. Finally, the sum of panels e and f, in panel g, is for comparison with the only remaining term, the local acceleration, in panel h. Closure is observed showing that the calculation is performed correctly. The lead terms are the Coriolis and pressure gradient terms. The ageostrophic residual is accounted for primarily by the surface and bottom Ekman layers, and the only other term of substance is the local acceleration. The pressure gradient is maximum near the coast and it decreases to zero by about the 50 m isobath. Modified by surface and bottom friction, the coastal jet seen in the Coriolis term follows the pressure gradient. The pressure gradient is relatively depth independent, i.e., it is primarily barotropic consistent with the Burger number arguments of Clarke and Brink (1985). The pressure gradient, however, does decrease across the bottom Ekman layer due to the sloping isopycnals there.

The comparable analysis for the peak upwelling event of day 12 is shown in Figure 13. The ordering of terms is the same as in Figure 12. The difference is in the magnitude and the offshore scale of the Coriolis and pressure gradient terms. Here the pressure gradient nodal line extends out to the 100 m isobath, the coastal jet is much stronger, and hence the bottom Ekman layer is much more developed. Opposite to the downwelling case, the pressure gradient increases across the bottom Ekman layer due to the slope of the isopycnals there. We will return to this point in section 7.

Our analysis of the vertically integrated, vertical component of vorticity is similar to that of Ezer and Mellor (1994). Taking the curl of the vertically integrated momentum equations, we discuss the vorticity balance with respect to four terms: 1) stress torque, 2) bottom pressure torque, 3) stretching of planetary vorticity by free surface deformation (plus the planetary beta effect), and 4) the material rate of change of relative vorticity (plus the stretching and tilting of relative vorticity by the flow field). Since we employed a spatially uniform wind stress, the stress torque is entirely due to bottom stress. The bottom pressure torque, through the bottom kinematic boundary condition, is the stretching of planetary vorticity by geostrophic flow across the sloping bottom. This is generally much larger than the stretching by free surface deformation (or by the planetary beta effect that we lumped together with free surface term). The residual of these tendencies is the variation in relative vorticity (that we lumped together with the kinematical terms associated with the flow field deformations of relative vorticity and with the relatively insignificant horizontal diffusion terms).

These four terms calculated at the 20 m isobath offshore of Sarasota, FL. for April 1998 are given in Figure 14. The bottom stress and bottom pressure torques are the lead terms, although the other two terms may be of comparable magnitude during the transitions when the sea surface slope is rapidly changing and the coastal jets are weak. Since these time series are spatially dependent their horizontal fields help to define the inner-shelf.

Figure 15 shows the four fields for the day 9 peak downwelling response. Once the pressure field and coastal jets are established, the inner-shelf is the region where the primary vorticity balance is between the bottom stress and bottom pressure torques. At this time the stretching of planetary vorticity by free surface deformation is small everywhere except for regions of strong eddies that form along the shelf break. The bottom pressure torque is large everywhere, but this tendency to induce relative vorticity can only be offset where large near bottom currents are capable of producing large bottom stresses, i.e., only in the inner-shelf region for this local wind forced experiment. Elsewhere the imbalance in these vorticity tendency terms leads to a large material rate of change of relative vorticity. Thus, the primary balance for the inner-shelf is between the bottom stress and bottom pressure torques, whereas the primary balance for the shelf-break is between bottom pressure torque and material rate of change of relative vorticity. Similar field representations for the day 12 peak upwelling response are shown in Figure 16. The conclusions are the same as with Figure 15 with the added point of asymmetry. The offshore scale of the inner-shelf is larger for the day 12 upwelling response than it is for the day 9 downwelling response.

How water move across the shelf is the underlying physical oceanographic question pertinent to multidisciplinary continental shelf studies. Boundary layer and eddy transport processes are involved because of the vorticity constraint by the sloping bottom. Understanding these processes presupposes an understanding of the shelf responses to its various forcing agents: momentum input at the sea surface and shelf break and buoyancy input at the sea surface, shelf break, and land. Since each continental shelf is different, and since so many processes are involved, it is useful to isolate regions and forcing conditions to answer smaller subsets of questions. Along this vein we focus on the WFS, which is wide enough for its inner-shelf to be distinguished from the shelf-break. Using in-situ data and a numerical model simulation we ask how well the currents over the inner-shelf are accounted for by local wind forcing alone. In doing this we describe the boundary layer effects that account for the transports across the inner-shelf, provide a dynamical definition of the inner-shelf, and describe an asymmetry in the inner-shelf responses to upwelling versus downwelling favorable winds.

The model and in-situ data comparison shows that a primitive equation model (in this case the sigma coordinate POM with Mellor/Yamada turbulence closure) is effective at describing the sea level and circulation of the inner-shelf when forced by local winds only. We conclude that local winds are a major driver of the inner-shelf circulation. However, stratification impacts the nature of the circulation and the across-shelf transports, and it does this by affecting turbulence and hence the vertical scales of the surface and bottom Ekman layers. When these layers are vertically constrained, through the suppression of turbulence by stratification, the velocity vector turning within the boundary layers increases over that for constant density. Stratification, in this way, largely increases across-shelf mass transport in response to local wind forcing.

Flow field kinematics and dynamics analyses show the WFS circulation to be fully three-dimensional (along-shore variations are significant). These analyses define the inner-shelf as the region where the surface and bottom Ekman layers play an important role in the momentum balance. Kinematically the inner-shelf is where the Ekman layers induce a sea surface slope through divergence. With respect to vertically integrated vorticity the inner-shelf is the region where the primary balance is between bottom stress and bottom pressure torques, as contrasted with the shelf break where the primary balance is between the bottom pressure torque and the material rate of change of relative vorticity.

An asymmetry is found in the WFS response to upwelling and downwelling favorable winds, wherein the magnitude and offshore extent of the responses to upwelling favorable winds exceed those for downwelling favorable winds under stratified conditions. While this asymmetry appears in all of the dynamical analyses, these analyses alone do not provide an explanation. The asymmetry is due to stratification as demonstrated by comparing model twin experiments, one with and the other without stratification. Asymmetry only occurs in the stratified experiment.

While we are not aware of such downwelling/upwelling asymmetry being reported elsewhere, MacCready and Rhines (1991) and Garrett et al. (1993) provide a conceptual and analytical basis for it. Their argument is that stratification impedes across-shelf transport in the bottom Ekman layer on a slope when the buoyancy force tends to balance the Coriolis force of the along-shelf velocity component. We diagnose this concept from both momentum and vorticity perspectives. With respect to momentum, the sea level response to downwelling winds results in an offshore directed pressure gradient force that drives the offshore directed flow in the bottom Ekman layer. Isopycnals bending into the bottom result in a buoyancy force that opposes this (Figure 12). In contrast to downwelling, the sea level response to upwelling winds results in an onshore directed pressure gradient force that drives an onshore directed flow in the bottom Ekman layer. Isopycnals bending into the bottom now result in a buoyancy force that enhances this (Figure 13). Granted, fewer isopycnals bend into the bottom; nevertheless the ones that do act constructively rather than destructively.

The simplest explanation for the asymmetry derives from the streamwise component of vorticity. For a stratified Ekman layer we consider the balance between the tendencies to induce relative vorticity by: 1) the tilting of planetary vorticity by the vertically sheared along-shelf jet, 2) the buoyancy torque by the sloping isopycnals, and 3) the dissipation of relative vorticity by the vertically sheared across-shelf flow. Equation (1) expresses this balance, with terms 1-3 on the left hand side and the local rate of change of relative vorticity, plus the omitted residual terms on the right hand side:

(1)

where , are the across-shelf and along-shelf velocity components, respectively, is density, is the vertical eddy coefficient, and is the residual. For downwelling, planetary vorticity tilting tends to be balanced by buoyancy torque, requiring less relative vorticity dissipation. For upwelling, the buoyancy torque, while reduced in magnitude from the downwelling case, adds to the planetary vorticity tilting, requiring increased relative vorticity dissipation. We demonstrate these effects in Figure 17 by comparing the peak downwelling and upwelling responses on days 9 and 12, respectively. Destructive interference between planetary vorticity tilting and buoyancy torque is observed for downwelling, versus constructive interference for upwelling. Similar results (not shown) are found for the other two downwelling and upwelling pairs. The buoyancy torque (by isopycnals bending into the sloping bottom) has the same sign for downwelling and upwelling, whereas the tilting term reverses sign.

A corollary affect, expanded on by Garrett et al. (1993) in relationship to the Lentz and Trowbridge (1991) and Trowbridge and Lentz (1991) findings, is an asymmetry in the bottom boundary layer vertical scale due to the stabilizing/destabilizing influences of up and down slope flows. While related, this is a different phenomenon that appears to be contrary to our finding (in Figure 11) that the bottom boundary layer scale is actually larger for upwelling. We reconcile this discrepancy by noting that our larger boundary layer scale for upwelling follows from the larger upwelling response. Had the upwelling and downwelling responses on the WFS been of equal magnitude with regard to the interior along-shelf flows, as in the numerical experiments reported by Garrett et al. (1993), then we would have expected results similar to theirs. Asymmetry in the bottom boundary layer is important in nature for the reasons espoused in these earlier papers, including Weatherly and Martin (1978).

The inner-shelf provides added importance to these stratified boundary layer concepts on a slope. For the inner-shelf, the surface pressure gradient set up by surface Ekman layer divergence, the geostrophic interior flow adjustment to the pressure gradient, and the bottom Ekman layer reaction to the interior flow all occur nearly in unison. Anything that impedes one of these three steps will impede all of them. Thus, by inhibiting (or promoting) the bottom Ekman layer, thereby reducing (or increasing) the near bottom divergence that is necessary to feed the near surface divergence, stratification produces the asymmetry in the magnitude and offshore extent of the responses to downwelling and upwelling favorable winds.

A physical consequence of asymmetry is the rectification of the shelf response to oscillatory winds. This provides a possible explanation of why the region south of Tampa Bay was found by Yang et al. (1999) to be devoid of surface drifter tracks during a year-long set of deployments. Stratification-induced asymmetry may also have important biological, chemical, and geological consequences. In analogy to a flapper valve, with upwelling responses favored over downwelling responses, near bottom material properties are more readily transferred into, than away from, the near-shore zone. Support for this comes from unpublished hydrographic data (G. Vargo, personal communication) that shows large chlorophyll fluorescence extending across the shelf in the bottom Ekman layer. In the along-shelf direction the rectification of material property transports by the coastal jets may also be important; impacting, for instance, long-term sediment transport. Further theoretical and observational studies are needed to explore the ramifications of stratification induced asymmetry on the continental shelf.

A related conclusion is that the seasonal and synoptic scales can not be fully separated. With synoptic scale wind forced responses dependent on stratification, it is necessary to either assimilate density data into a model, or simulate density changes through a combination of surface buoyancy fluxes and active offshore boundary conditions. In our case, a 45 day (15 days of start-up and 30 days of analysis) simulation worked well, whereas attempts to carry the model integration longer met with increasing deviations from the in-situ data due to density field changes. Nowcasting and forecasting of the inner-shelf must be supported by sufficient in-situ data for density field assimilation and boundary conditions.

Acknowledgements. Support for this work derived from the Office of Naval Research, grant N00014-98-1-0158; the National Oceanic and Atmospheric Administration, grant NA76RG0463; and the Minerals Management Service, contract MMS 14-35-0001-30804. G. Mitchum offered helpful discussions; R. Cole, J. Donovan, R. He, and W Hemme assisted with the data collection and analyses.

Allen, J.S., P.A. Newberger, and J. Federiuk, Upwelling circulation on the Oregon
         continental shelf. Part I: response to idealized forcing, J. Phys. Oceanogr., 25,
         1843-1866, 1995.

Blumberg, A.F. and G.L. Mellor, A description of a three-dimensional coastal ocean
         circulation model, in Three-dimensional Coastal Ocean Models, Vol. 4, N. Heaps
         (ed.), 208-233, AGU, Washington, D. C., 1987.

Brink, K.H., Wind-driven currents over the continental shelf, in The Sea Vol. 10, K.H. Brink and
         A. Robinson, (eds.), Wiley, New York, 1998.

Clarke, A.J., and K.H. Brink, The response of stratified, frictional flow of shelf and slope
         waters to fluctuating large-scale, low-frequency wind forcing, J. Phys. Oceanogr.,
         15, 439-453, 1985.

Clarke, A. J., and S. Van Gorder, A method for estimating wind-driven frictional, time-
         dependent, stratified shelf and slope water flow, J. Phys. Oceanogr., 16, 1013-1027, 1986.

Csanady, Circulation in the Coastal Ocean, Reidel, Dordrecht, Netherlands, pp., 1982.

Ezer, T. and G.L. Mellor, Diagnostic and prognostic calculations of the North Atlantic
         circulation and sea level using a sigma coordinate ocean model, J. Geophys. Res., 99,
         14159-14171, 1994.

Garrett, C., P. MacCready, and P. Rhines, Boundary mixing and arrested Ekman layers: Rotating
         stratified flow near a sloping boundary, Annu. Rev. Fluid Mech., 25, 291-323, 1993

Gilbes, F., C. Tomas, J.J. Walsh, and F. Muller-Karger, An episodic chlorophyll plume on the
         west Florida shelf, Cont. Shelf Res., 16, 1201-1224, 1996.

Gill, A.E., Atmosphere-Ocean Dynamics, Academic Press, New York, 662pp., 1982

Lentz, S.J., The surface boundary layer in coastal upwelling region, J. Phys. Oceanogr., 22,
         517-1539, 1992.

Lentz, S.J., Current dynamics over the northern California inner shelf, J. Phys. Oceanogr,
         24, 2461-2478, 1994.

Lentz, S.J., Sensitivity of the inner shelf circulation to the form of the eddy viscosity profile, J.
         Phys. Oceanogr, 25, 19-28, 1995.

Lentz, S.J., and J.H. Trowbridge, The bottom boundary layer over the northern California
         shelf, J. Phys. Oceanogr., 21, 1186-1202, 1991.

Lentz, S.J., R.T. Guza, S. Elgar, F. Feddersen, and T.H.C. Herbers, Momentum balances on the
         North Carolina inner shelf., J. Geophys. Res., 104, 18205-18226, 1999.

Li, Z., Upwelling circulation on the west Florida continental shelf, Ph.D. thesis, University
         of South Florida, St. Petersburg, Florida, 309 PP, 1998.

Li, Z, and R. H. Weisberg, WFS response to upwelling favorable wind forcing: Kinematics,
         J. Geophys. Res., 104, 13507-13527, 1999.

Li, Z, and R. H. Weisberg, WFS response to upwelling favorable wind forcing: Dynamics,
         J. Geophys. Res., 104, 23427-23442, 1999.

Lopez, M. and Clarke, A.J., The wind-driven shelf and slope water flow in terms of a local and a
         remote response, J. Phys. Oceanogr., 19, 1091-1101, 1989.

MacCready, P. and P.B. Rhines, Buoyant inhibition of Ekman transport on a slope and its effect
         on stratified spin-up, J. Fluid Mech., 223, 1991

Mellor, G.L. and T. Yamada, Development of a turbulence closure model for geophysical fluid
         problems, Rev. Geophys., 20, 851-875.

Mitchum, G.T., and W. Sturges, Wind-driven currents on the west Florida shelf, J. Phys.
         Oceanogr., 12, 1310-1317, 1982.

Mitchum, G.T., and A.J. Clarke, The frictional, near shore response to forcing by synoptic scale
         winds , J. Phys. Oceanogr., 16, 1029-1037, 1986.

Mitchum, G.T., and A.J. Clarke, Evaluation of frictional, wind forced long wave theory on
         the West Florida shelf, J. Phys. Oceanogr., 16, 934-946, 1986.

Munchow, A., and R.J. Chant, Kinematics of inner shelf motions during the summer
         stratified seasons off New Jersey, J. Phys. Oceanogr., 30, 247-268, 2000.

Samelson, R.M., Coastal boundary conditions and the baroclinic structure of wind-driven
         continental shelf currents, J. Phys. Oceanogr., 27, 2645-2662, 1997.

Smith, R.L., The physical processes of coastal ocean upwelling systems, in Upwelling in
         the Ocean: Modern Processes and Ancient Records, Summerhayes et al. (eds.),
         39-64, 1995.

Trowbridge, J.H., and S.J. Lentz, Asymmetric behavior of an oceanic boundary layer above
         a sloping bottom, J. Phys. Oceanogr., 21,1171-1185, 1991.

Walsh, J.J., On the Nature of Continental Shelves, Academic Press, San Diego, 520pp, 1988.

Weatherly, G.L., and P.J. Martin, On the structure and dynamics of the oceanic bottom
         boundary layer, J. Phys. Oceanogr., 8, 557-570, 1978.

Weatherly, G.L., and D. Thistle, On the wintertime currents in the Florida Big Bend region,
         continental Shelf Research, 17, 1297-1319, 1997.

Weisberg, R.H., B.D. Black, and H. Yang, Seasonal modulation of the west Florida shelf
         circulation, Geophys. Res. Lett., 23, 2247-2250, 1996.

Weisberg, R.H., B.D. Black, and Z. Li, An upwelling case study on Florida’s west coast,
         J. Geophys. Res., 105, 11459-11469, 2000.

Wu, J., Wind-stress coefficients over sea surface near neutral conditions—A revisit, J. Phys.
         Oceanogr., 10, 727-740, 1980.

Yang, H., R.H. Weisberg, P.P. Niiler, W. Sturges, and W. Johnson, Lagrangian circulation and
         forbidden zone on the west Florida shelf, Cont. Shelf Res., 19, 1221-1245, 1999.

Yankovsky, A.E., and R.W. Garvine, Subinertial dynamics on the inner New Jersey shelf
         during the upwelling season, J. Phys. Oceanogr., 28, 2444-2458, 1998.

Figure 1 West Florida shelf bathymetry and the measurement locations (upper panel) and numerical model domain with coordinate system description as applied herein (lower panel). The model seaward boundaries are open except for the southeast corner where the solid line represents closure by the Florida Keys. The solid line offshore from Sarasota denotes the section sampled for kinematical and dynamical analyses.

Figure 2 April 1998 measurements of: a) along-shelf and b) across-shelf velocity components sampled at the 20 m isobath offshore of Sarasota FL., c) sea level at St. Petersburg, d) wind velocity sampled at NOAA buoy 42036, and e) wind stress. The contour intervals are 0.05 ms^-1 for the velocity components, north is up and east is to the right for the wind vectors, and all data are low pass filtered to exclude oscillations at time scales shorter than 36 hours.

Figure 3 Modeled (dashed-doted lines) and observed (solid lines) sea level variability for the constant density (panel a) and stratified (panel b) cases, along with the April 1998 wind vectors.

Figure 4a April 1998 stratified model simulations of: a) along-shelf and b) across-shelf velocity components, and c) isopycnal variations sampled at the 20 m isobath offshore of Sarasota FL, along with the wind vectors used to drive the model (with north up and east to the right). The contour intervals are 0.05 ms^-1 for the velocity components and sigma units for the density.

Figure 4b April 1998 constant density model simulations of: a) along-shelf and b) across-shelf velocity components sampled at the 20 m isobath offshore of Sarasota FL, along with the wind vectors used to drive the model (with north up and east to the right). The contour intervals are 0.05 ms^-1 for the velocity components.

Figure 5a Daily snapshots of the stratified model simulated WFS sea surface topography spanning the period of downwelling and upwelling between days 7 to 14. The contour interval is 0.02 m, and the ranges for sea level are given in parentheses.

Figure 5b Daily snapshots of the constant density model simulated WFS sea surface topography spanning the period of downwelling and upwelling between days 7 to 14. The contour interval is 0.02 m, and the ranges for sea level are given in parentheses.

Figure 6a Daily snapshots of the along-shelf, across-shelf, and vertical velocity components and density sampled along a cross section offshore of Sarasota, FL. spanning the period of downwelling and upwelling between days 7 to 13. The contour intervals are 0.05 ms^-1 for the horizontal velocity components, 10^-5 msec^-1 for the vertical velocity component, and sigma units for density.

Figure 6b Daily snapshots of the along-shelf, across-shelf, and vertical velocity components for the constant density case, sampled along a cross section offshore of Sarasota, FL. spanning the period of downwelling and upwelling between days 7 to 13. The contour intervals are 0.05 ms^-1 for the horizontal velocity components and 10^-5 msec^-1 for the vertical velocity component.

Figure 7 April 1998 measurements of: a) along-shelf and b) across-shelf velocity components sampled at the 50 m isobath offshore of Tampa Bay. The contour intervals are 0.05 ms^-1 for the velocity components, north is up and east is to the right for the wind vectors, and all data are low pass filtered to exclude oscillations at time scales shorter than 36 hours.

Figure 8 Horizontal velocity vector fields: a) depth-averaged, b) near surface, c) mid-water, and d) near bottom, sampled during the peak downwelling event on day 9. Vectors are shown for every other grid point with the maximum value for each panel given in the panel legend. The near bottom vectors are magnified by a factor of two relative to the other panels.

Figure 9 Horizontal velocity vector fields: a) depth-averaged, b) near surface, c) mid-water, and d) near bottom, sampled during the peak upwelling event on day 12. Vectors are shown for every other grid point with the maximum value for each panel given in the panel legend. The near bottom vectors are magnified by a factor of two relative to the other panels.

Figure 10a Satellite AVHRR temperature image for April 10^th, the time of warmest SST associated with the peak downwelling of day 9.

Figure 10b Satellite AVHRR temperature image for April 13^th, the time of coldest SST associated with the peak upwelling of day 12.

Figure 11 Time series of the vertically integrated: a) along-shelf and b) across-shelf momentum balance terms and the c) across-shelf transports, along with d) the across-shelf ageostrophic momentum residual, all sampled at the 20 m isobath offshore of Sarasota FL. from the stratified model simulation

Figure 12 The across-shelf momentum balance during the peak downwelling event on day 9 sampled offshore from Sarasota FL. from the stratified model simulation. The panels are: a) Coriolis; b) pressure gradient; c) their sum, or the ageostrophic residual; d) friction (primarily vertical); e) the sum of the Coriolis, pressure gradient, and friction terms; f) advective acceleration; g) the sum of e and f; and h) the local acceleration. Contour intervals are given in each panel and shaded regions are negative.

Figure 13 The across-shelf momentum balance during the peak upwelling event on day 12 sampled offshore from Sarasota FL. from the stratified model simulation. The panels are: a) Coriolis; b) pressure gradient; c) their sum, or the ageostrophic residual; d) friction (primarily vertical); e) the sum of the Coriolis, pressure gradient, and friction terms; f) advective acceleration; g) the sum of e and f; and h) the local acceleration. Contour intervals are given in each panel and shaded regions are negative.

Figure 14 Time series of the vertically integrated vorticity balance terms sampled at the 20 m isobath offshore of Sarasota FL. from the stratified model simulation.

Figure 15 Horizontal distribution fields for the vertically integrated vorticity balance terms during the peak downwelling event on day 9: a) the material rate of change, plus tilting and stretching of relative vorticity; b) the stretching of planetary vorticity by changes in the free surface, plus the planetary beta terms; c) the bottom pressure torque; and d) the bottom stress torque. Contour intervals and ranges are given with each panel and shaded regions are negative.

Figure 16 Horizontal distribution fields for the vertically integrated vorticity balance terms during the peak upwelling event on day 12: a) the material rate of change, plus tilting and stretching of relative vorticity; b) the stretching of planetary vorticity by changes in the free surface, plus the planetary beta terms; c) the bottom pressure torque; and d) the bottom stress torque. Contour intervals and ranges are given with each panel and shaded regions are negative.

Figure 17 An analysis of the along-shelf component of vorticity during the peak downwelling and upwelling responses on a) day 9 and b) day12, respectively. From left to right in each panel are 1) the tilting of planetary vorticity filaments by the sheared along-shelf jet, 2) the buoyancy torque, 3) the dissipation of relative vorticity by the sheared across-shelf flow, and 4) the local rate of change of relative vorticity, plus the remainder of other omitted terms. The contour interval is 10^-7 s^-2.